3.2.8: The Concept of a Cutoff Grade
We know that orebody characteristics such as the grade vary spatially within the orebody, and as we approach the boundaries of the deposit, the grade will begin to decrease to zero. Eventually, the cost to mine and process a ton of ore will exceed the value that we can obtain by selling the commodity found in that ton of ore. Mining companies, like other businesses, do not stay in business by selling their product at a loss!
Thus, when we are estimating the amount of the resource that can be mined economically, we’ll have to calculate a cutoff grade; and any ore with a grade lower than the cutoff cannot be counted in the estimate of the reserve. The cutoff grade is the grade at which the cost of mining and processing the ore is equal to the desired selling price of the commodity extracted from the ore.
The cutoff grade is influenced by a few external factors that you can control to a certain extent, and these will be considered in the prefeasibility analysis when the cutoff grade is determined.
Let’s imagine that we have a deposit of copper that we are evaluating. It is a large resource with a grade of 1%. The block below represents 1 ton (T) of in-place ore. We know that the grade is 1%, so we have 20 lb. of copper distributed in that ton of ore. Let’s represent that 20 pounds of copper as a small (not-to-scale) block inside of the larger block.

Figure 3.2.14: Figure 6 from the text
When we mine this ton of ore, it is likely that we will get some dilution, which occurs when we extract some of the rock surrounding the orebody. In other words we are diluting our ore with this host rock. Why would we do that? We don’t do it on purpose, generally, but, it is a consequence of the mining method and equipment that we select to mine the ore. Imagine that you have a chocolate cake, and this cake has a thin band of raspberry filling in the middle of the cake. Suppose that you are tasked with removing the raspberry layer, and that you do not want to have any of the chocolate layers mixed with the raspberry layer that you are extracting. Further, I will give you a tiny, baby-sized spoon to complete the task on your cake, and I will give your classmate a large serving-size scoop to complete the task on his cake. You both have ten minutes to complete the job, with a goal of minimizing the dilution of the raspberry layer with the chocolate cake..
The outcome of this experiment is evident. The use of the tiny, rather than large spoon will allow the competitor to be more exacting in the removal of the raspberry layer, resulting in far less contamination, i.e. dilution, of the product. In mining terms, we refer to this as the selectivity of the mining method, and some methods are much more selective than others, resulting in far less dilution. Of course, there are tradeoffs between selectivity and other important metrics such as mining cost and productivity. We’ll look closely at this when we study the mining methods. Now, we can continue with our example.
We extract one ton of material, and now we know that this one-ton of material will be diluted with non-ore bearing material, based on how selective our mining method is estimated to be. We can represent this as shown in Figure 3.2.15 by including the waste within the one ton of mined ore. This waste material effectively reduces the copper in the block by the amount of the dilution. Let’s assume an average dilution of 5%. The copper present in the mined block of ore is reduced by 5%, to 19 lb of copper.
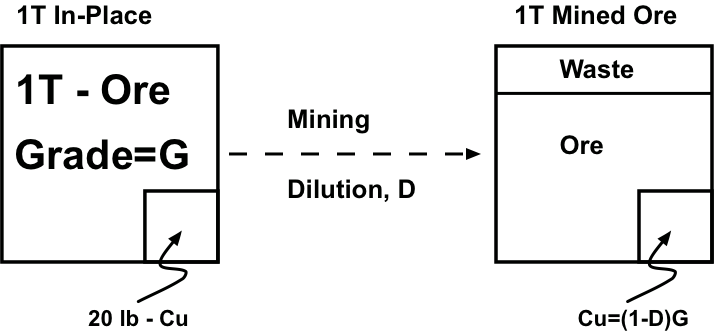
Figure 3.2.15: Figure 7 from the text
Next, our one-ton block of mined material will be routed into the mineral processing plant, where the ore will be separated and concentrated into a saleable product. There will be two output streams from the plant: one containing the saleable product and the other, the tailings, or waste. The physical and chemical methods used to beneficiate the ore are not perfect, and while we can invest more money to improve them, there is a point of diminishing return. Consequently, some saleable product will report to the waste stream, and as such represents a loss. Let’s assume a plant recovery of 90%, meaning that all but 10% of the product in the plant feed will be recovered and report to the product stream. In our example, there is 19 lb. of copper in the feed to the plant and the plant will recover all but 1.9 lb. Thus, the one ton of material that we mined will yield 17.1 lb of copper for sale.
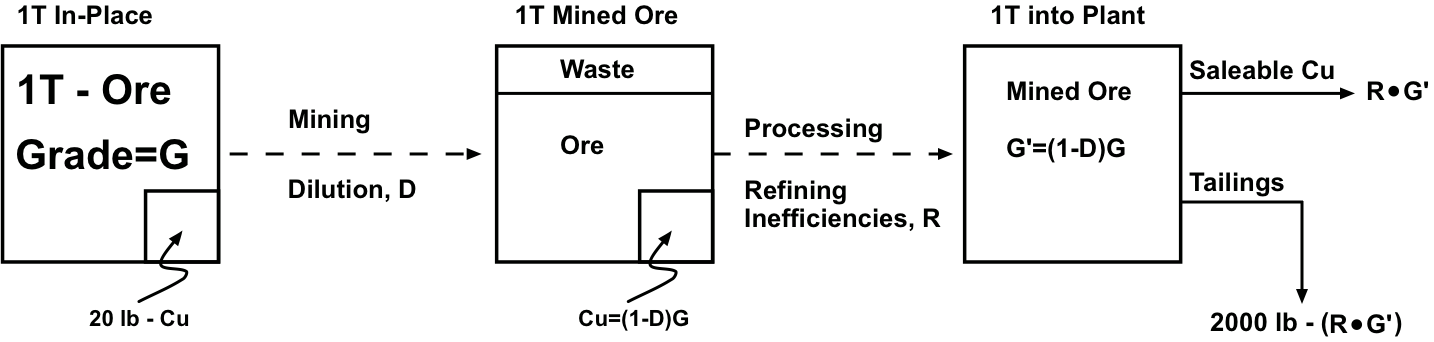
Figure 3.2.16: Figure 8 from the text
Mathematically, the minimum acceptable grade to mine, i.e. the cutoff grade, occurs when the cost to mine and process the material, (M&P cost), is equal to the value of the product, i.e. its selling price, SP.
M & P cost = SP
(Equation 3.2.9)
We will account for the dilution and recovery losses in the right side of the equation, as these losses are reducing the value of the in-place ore.
M&P cost=SP*(1-D)*(R)*G
(Equation 3.2.10)
where:
- M&P cost = mining & processing cost, $/T
- SP = selling price of the copper, $/lb
- D = dilution
- R = plant recovery
- G = grade
Let’s use some numbers. Assume the following: we have a dilution of 5%, a plant recovery of 92%, a mining and processing cost of $6.80/ton and a selling price of $0.74/lb. Be careful with the units!
Solving the equation for grade, we have:
G=(M&P cost)/{SP*(1-D)*R}
(Equation 3.2.11)
And substituting our values,
G=($6.80/T){$0.74/lb*(1−0.05)*(0.92)*(2000lb/T)}
G=0.499≅0.5=.5%
Therefore for this example, the grade of the ore that we choose to mine must have a grade of 0.5% of greater. In other words, the cutoff grade has been determined to be 0.5%, and when you report the size of your reserve, you will include only the tonnage at or greater than 0.5%. Do you understand why you must report it in that way?
Imagine a situation in which your resource contains significant tonnage at slightly less than 0.5%. Likely you will reexamine your dilution and plant recovery assumptions, and explore options for improving both so that you can economically mine the lower grade ore.
We didn’t say much about the selling price itself. Presumable, it is the maximum price that we believe we can reasonably expect to sell our product into the market. The price will need to cover not only our mining and processing costs, but also whatever profit we require. When companies evaluate the merits of opening a new mine they will have certain criteria for establishing the financial merits of the project. They might, for example, require a certain return on their invested capital, a payback within so many years, and so forth. This can all be bundled, at least conceptually, into the required selling price.
Sometimes we will talk about the gross value of the mined ore. The gross value is equal to:
=(G)*(1−D)*(R)*(SP)
(Equation 3.2.12)
The unit profit is then defined as: Gross Value – Mining & Processing Cost.
To illustrate, assume that we are mining an orebody with a grade of 1.2%, dilution is negligible, and the selling price is $0.74/lb. The gross value is calculated to be $16.34/T and the unit profit is $9.54.